Ray Mini-Course

Aru Ray
Topological 4-manifolds: the disc embedding theorem and beyond

Abstract: In 1982 Freedman proved the 4-dimensional Poincare conjecture in the topological category. The key tool in the proof was the disc embedding theorem, which allows a topological version of the Whitney trick in certain cases in dimension four. Freedman’s work was significantly extended by Quinn, who established fundamental results in topological 4-manifolds, such as topological transversality, and smoothing results for noncompact 4-manifolds.

We will begin with an account of the work of Freedman and Quinn, followed by classification results for topological 4-manifolds. We will focus on the applications of the Freedman-Quinn technology and compare with what is known in higher (and lower) dimensions. Finally, we will state and discuss the open problems in the field, the most significant of which, remarkably, take the form of slicing problems for knots and links.

A more detailed outline and typewritten lecture notes can be found here

TAs for this course will be Patrick Orson (ETH Zurich) and Benjamin Ruppik (MPIM)

Combine lecture notes for all 5 lectures is available here: Ray

Lecture 1

Part a: Mini-course overview

Part b: Proof of the high-dimensional h-cobordism theorem

Part c: Proof of Wall’s theorem + sketch of proof of cork theorem

Lecture notes are available here Ray 1

Lecture 2

Part a: Visualising surfaces in dimension four

Part b: Proof of Freedman’s h-cobordism theorem

Part c: Outline of proof of the disc embedding theorem

Lecture notes are available here Ray 2

Lecture 3

Lecture notes are available here Ray 3

Lecture 4

Lecture notes are available here Ray 4

Lecture 5

Lecture notes are available here Ray 5

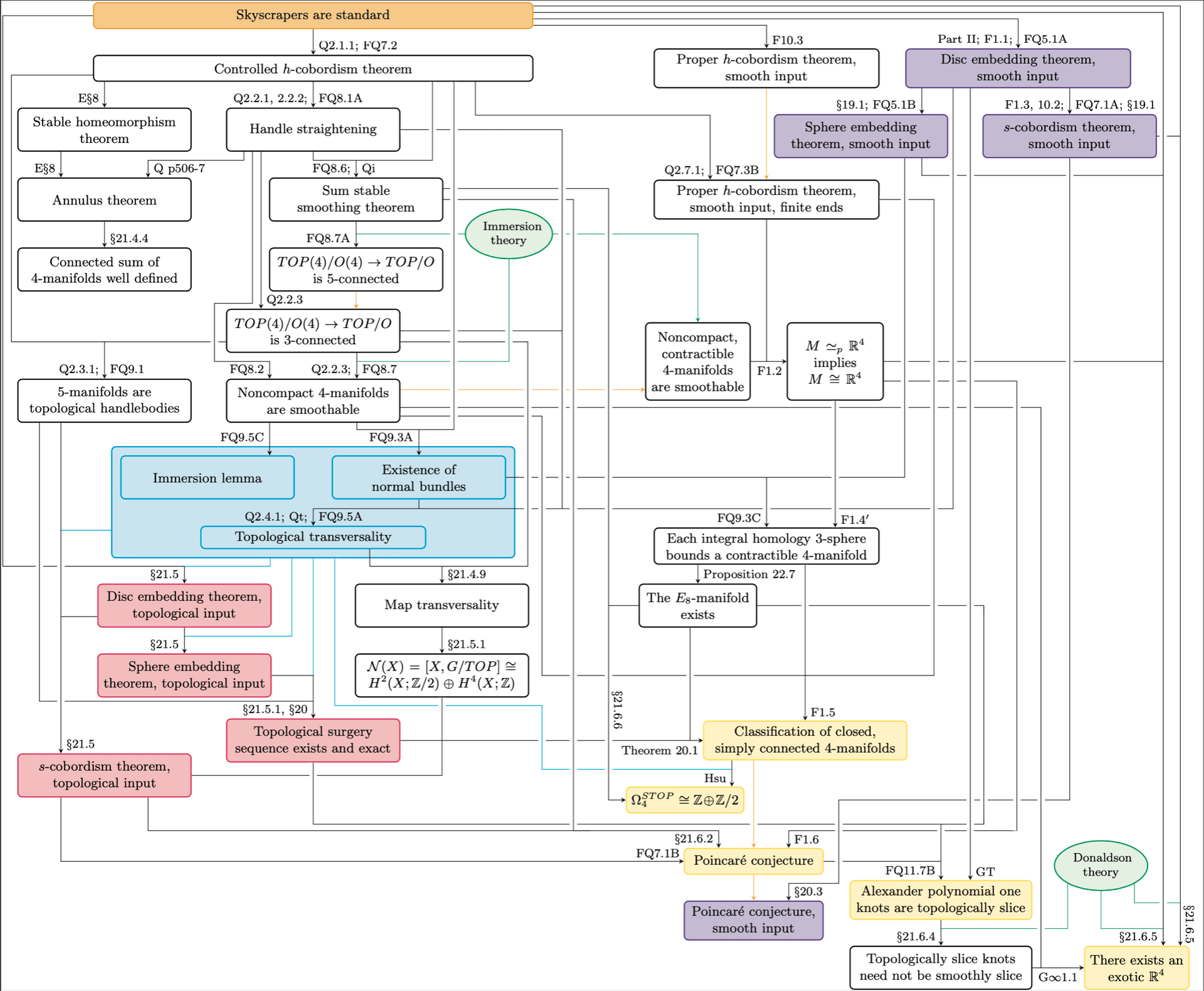
Here is the “not a conspiracy theory” chart from Aru’s talk